LIMITS OF FUNCTIONS USING THE SQUEEZE PRINCIPLE

Math AP®︎/College Calculus AB Limits and continuity Determining limits using the squeeze theorem Squeeze theorem AP.CALC: LIM‑1 (EU), LIM‑1.E (LO), LIM‑1.E.2 (EK). !0 1 = 1, the Squeeze Theorem allows us to conclude that lim!0 sin = 1: 3.Use the previous example to evaluate lim x!0 sin(4x) sin(6x); if this limit exists. (Solution)For x6= 0 we can rewrite this quotient as sin(4x) sin(6x) = xsin(4x) xsin(6x) = 4 6 6x sin(6x) sin(4x) 4x: Then lim x!0 sin(4x) sin(6x) = 4 6 lim x!0 6x sin(6x) lim x!0 sin(4x) 4x = 4 6 lim x!0 sin(6x) 6x 1 lim x!0. The squeeze theorem is a very useful theorem to quickly find the limit. However, finding the upper and lower bound functions can be hard. Sometimes graphing f(x) in order to see what the function approaches at x can be helpful when deciding what the lower and upper bounded functions should be.

The following problems involve the algebraic computation of limits using the Squeeze Principle,which is given below.

Ap Calculus Squeeze Theorem Worksheet

SQUEEZE PRINCIPLE : Assume that functions f , g , and h satisfy

and

.

Squeeze Theoremap Calculus Notes

Then

.

(NOTE : The quantity A may be a finite number, , or . The quantitiy L may be a finite number, , or .)

Squeeze Theoremap Calculus Test

The Squeeze Principle is used on limit problems where the usual algebraic methods (factoring, conjugation, algebraic manipulation, etc.) are not effective. However, it requires that you be able to ``squeeze' your problem in betweentwo other ``simpler' functions whose limits are easily computable and equal. The use of the Squeeze Principle requires accurate analysis, deft algebra skills, and careful use of inequalities.

• PROBLEM 1 : Compute .

  Click HERE to see a detailed solution to problem 1.
  

• PROBLEM 2 : Compute .

  Click HERE to see a detailed solution to problem 2.
  

• PROBLEM 3 : Compute .

  Click HERE to see a detailed solution to problem 3.
  

• PROBLEM 4 : Compute .

  Click HERE to see a detailed solution to problem 4.
  

• PROBLEM 5 : Compute .

  Click HERE to see a detailed solution to problem 5.
  

• PROBLEM 6 : Compute .

  Click HERE to see a detailed solution to problem 6.
  

• PROBLEM 7 : Compute .

  Click HERE to see a detailed solution to problem 7.
  

• PROBLEM 8 : Assume that exists and . Find .

  Click HERE to see a detailed solution to problem 8.
  

• PROBLEM 9 : Consider a circle of radius 1 centered at the origin and an angle of radians, , in the given diagram.
  

  
  

  a.) By considering the areas of right triangle OAD, sector OAC, and right triangle OBC, conclude that

  .

  b.) Use part a.) and the Squeeze Principle to show that

  Click HERE to see a detailed solution to problem 9.
  

• PROBLEM 10 : Assume that

  Show that f is continuous at x=0 .

  Click HERE to see a detailed solution to problem 10.

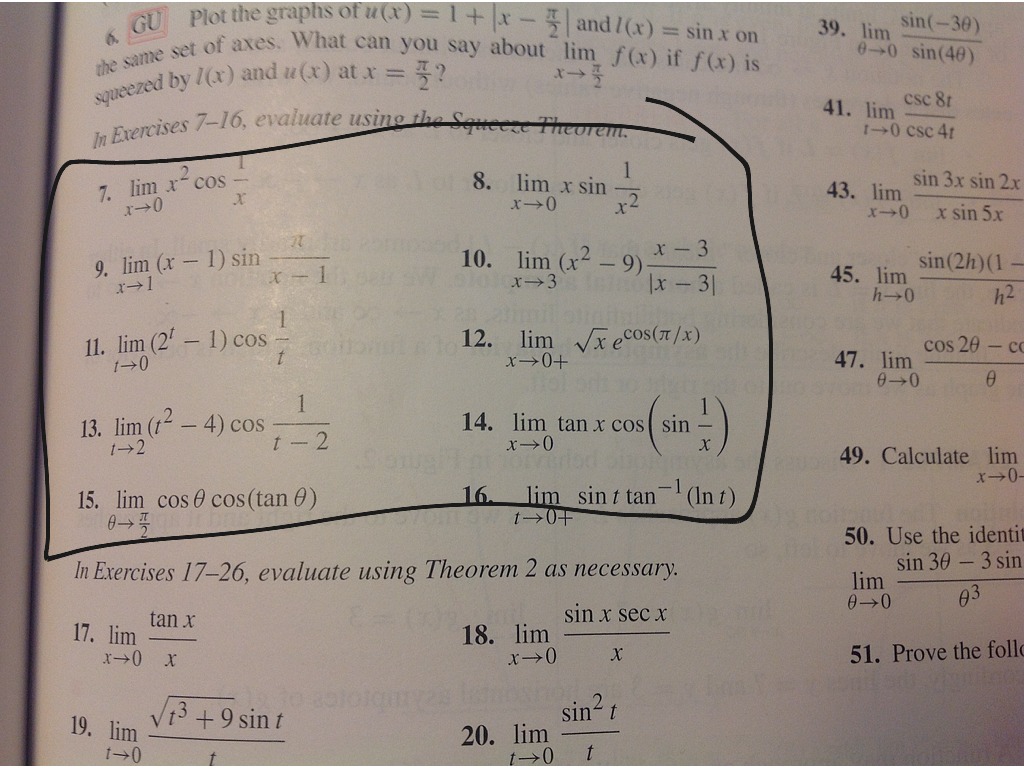
Click HERE to return to the original list of various types of calculus problems.

Your comments and suggestions are welcome. Please e-mail any correspondence to Duane Kouba by clicking on the following address :

Squeeze Theorem Ap Calculus

Duane Kouba
Wed Oct 15 16:55:51 PDT 1997